Chaos Game Analysis of Genomes

Triforce Power

Genomic code that makes us is made up of four letters, ATGC. Billions of these letters together creates a lifeform. Iterated function systems (IFS) are anything that can be made by repeating the same simple rules over and over. The easiest example being tree branches, add a simple structure repeatedly ad-infinitum and before you know it we have complex and beautiful systems; the popular example being the Sierpinski Triangle or “triforce” for the Zelda fans. As the cost of DNA sequencing becomes cheaper day by day we are confronted with a tsunami of data and it has become exceedingly difficult to derive meaningful answers from all the information contained within us.

H. Sapiens

Finding any advantage in ways to organize and view the data helps us discover minuet differences between individuals or say a normal cell versus a cancer cell. This is where Chaos Game Representation (CGR) becomes helpful, CGR is just a form of IFS that is helpful in mapping seemingly random information, that we suspect or know to have some sort of underlying structure.

In our case this would be the human genome. Although when looking at the letters coming from our DNA it seems like billions of random babbles, it is of course organized in a manner to give the blueprint for our bodies.  So let’s roll the dice-  do we get any sort of meaningful structure when applying CGR to DNA? If you are so inclined, something fun to try is the following:

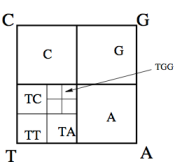
genome = Import["c:\data\sequence.fasta", "Sequence"];
genome = StringReplace[ToString[genome], {"{" -> "", "}" -> ""}];
chars = StringCases[genome, "G" | "C" | "T" | "A"];
f[x_, "A"] := x/2;
f[x_, "T"] := x/2 + {1/2, 0};
f[x_, "G"] := x/2 + {1/2, 1/2};
f[x_, "C"] := x/2 + {0, 1/2};
pts = FoldList[f, {0.5, 0.5}, chars];
Graphics[{PointSize[Tiny], Point[pts]}]

g1346a094 on Chromosome 7

For example, reading the sequence in order, apply T1 whenever C is encountered, apply T2 whenever A is encountered, apply T3 whenever T is encountered, and apply T4 whenever G is encountered. Really though any transformations to C, A, T, and G can be used and multiple methods can be compared. Self-similarity is immediately noticeable in these maps, which isn’t all that surprising since fractals are abundant in nature and DNA after all, is a natural syntax. Being aware that these patterns exist within our data, opens us up to some new questions to evaluate if IFS, CGR and fractals in general are helpful tools in the interpretation of genomic data.

Signal transducer 5B (STAT5B), on chromosome 17

Since the mapping is 1-1 and we see patterns emerge, we are hinted that there may be biological relevance; especially because different genes yield different patterns. But what exactly are the correlations between the patterns and the biological functions? It would also be very interesting to see mappings of introns/exons colored differently or color amino acids and various codons. One thing is for sure, genomes aren’t just endless columns and rows of letters, they are pictures. It is much easier to compare pictures and discover variations, which can ultimately allow us to find meaningful interpretation from this invaluable data.

Citations:

Jeffrey, H. J., “Chaos game visualization of sequences,” Computers & Graphics 16 (1992), 25-33.

Ashlock, D. Golden, J.B., III. Iterated function system fractals for the detection and display of DNA reading frame (2000) ISBN: 0-7803-6375-2

VV Nair, K Vijayan, DP Gopinath ANN based Genome Classifier using Frequency Chaos Game Representation (2010)